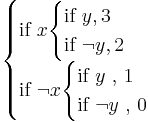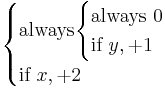Binary moment diagram

A binary moment diagram (BMD) is a generalization of the binary decision diagram (BDD) to linear functions over domains such as booleans (like BDDs), but also to integers or to real numbers.

They can deal with boolean functions with complexity comparable to BDDs, but also some functions that are dealt with very inefficiently in a BDD are handled easily by BMD, most notably multiplication.

The most important properties of BMD is that, like with BDDs, each function has exactly one canonical representation, and many operations can be efficiently performed on these representations.

The main features that differentiate BMDs from BDDs are using linear instead of pointwise diagrams, and having weighted edges.

The rules that ensure the canonicity of the representation are:

Decision over variables higher in the ordering may only point to decisions over variables lower in the ordering.
No two nodes may be identical (in normalization such nodes all references to one of these nodes should be replaced be references to another)
No node may have all decision parts equivalent to 0 (links to such nodes should be replaced by links to their always part)
No edge may have weight zero (all such edges should be replaced by direct links to 0)
Weights of the edges should be coprime. Without this rule or some equivalent of it, it would be possible for a function to have many representations, for example 2x + 2 could be represented as 2 · (1 + x) or 1 · (2 + 2x).

Pointwise and linear decomposition

In pointwise decomposition, like in BDDs, on each branch point we store result of all branches separately. An example of such decomposition for an integer function (2x + y) is:

$\begin{cases} \text{if } x \begin{cases} \text{if } y , 3 \\ \text{if } \neg y , 2 \end{cases} \\ \text{if } \neg x \begin{cases} \text{if } y \text{ , } 1 \\ \text{if } \neg y \text{ , } 0 \end{cases} \end{cases}$

In linear decomposition we provide instead a default value and a difference:

$\begin{cases} \text{always} \begin{cases} \text{always } 0 \\ \text{if } y , %2B1 \end{cases} \\ \text{if } x , %2B2 \end{cases}$

It can easily be seen that the latter (linear) representation is much more efficient in case of additive functions, as when we add many elements the latter representation will have only O(n) elements, while the former (pointwise), even with sharing, exponentially many.

Edge weights

Another extension is using weights for edges. A value of function at given node is a sum of the true nodes below it (the node under always, and possibly the decided node) times the edges' weights.

For example 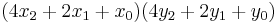$(4x_2 %2B 2x_1 %2B x_0) (4y_2 %2B 2y_1 %2B y_0)$ can be represented as:

Result node, always 1× value of node 2, if 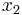$x_2$ add 4× value of node 4
Always 1× value of node 3, if 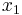$x_1$ add 2× value of node 4
Always 0, if 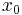$x_0$ add 1× value of node 4
Always 1× value of node 5, if 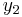$y_2$ add +4
Always 1× value of node 6, if 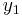$y_1$ add +2
Always 0, if 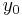$y_0$ add +1

Without weighted nodes a much more complex representation would be required:

Result node, always value of node 2, if 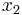$x_2$ value of node 4
Always value of node 3, if 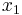$x_1$ value of node 7
Always 0, if 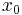$x_0$ value of node 10
Always value of node 5, if 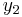$y_2$ add +16
Always value of node 6, if 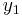$y_1$ add +8
Always 0, if 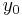$y_0$ add +4
Always value of node 8, if 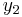$y_2$ add +8
Always value of node 9, if 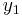$y_1$ add +4
Always 0, if 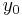$y_0$ add +2
Always value of node 11, if 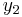$y_2$ add +4
Always value of node 12, if 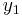$y_1$ add +2
Always 0, if $y_0$ add +1